1. 概述
傅里叶分析在过去两个世纪中吸引了众多研究者的关注。如今,傅里叶变换在许多实际应用中扮演着重要角色,远超傅里叶本人当初的设想!
在本教程中,我们将深入讲解傅里叶变换(Fourier Transform)的原理,并重点介绍其高效实现算法——快速傅里叶变换(Fast Fourier Transform, FFT):
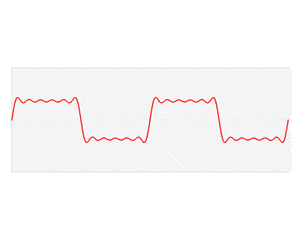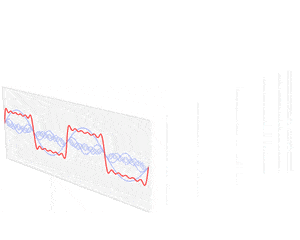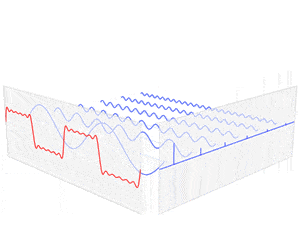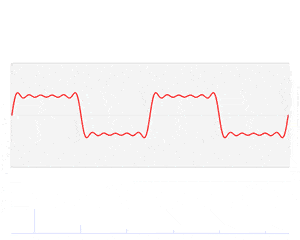
我们会从直观理解出发,解释其背后的数学原理,并结合两个实际应用场景说明其重要性。
2. 简介
将一个函数展开为多个更简单函数的线性组合,这一思想引导科学家们深入理解了多个领域,如泛音、无线频率、谐波、拍频、滤波器等。当傅里叶首次提出他的分析方法,并尝试用一系列周期函数的和来表示任意周期函数(例如:sin、cos)时,他遭到了许多质疑。
例如,当时物理学界的权威拉普拉斯就无法接受一个正弦函数能够表示一个余弦函数。直到1811年,傅里叶在原有基础上补充了傅里叶变换,才使得他的理论更具普适性——不仅适用于周期函数,也适用于非周期函数。
2.1. 傅里叶变换的计算
在信号处理和线性系统分析中,傅里叶变换的重要性早已被广泛认可。但在早期,由于计算离散傅里叶变换所需的运算量太大,其实用性受到了限制。直到James Cooley和John Tukey提出快速傅里叶变换(FFT)算法后,这一问题才得以解决。
3. 离散傅里叶变换(DFT)
离散傅里叶变换(DFT)对 n 个点的输入序列 a 的变换公式如下:
$$ A_i = \sum_{j=0}^{n-1} \omega_n^{ij} a_j, \quad i = 0, 1, ..., n-1 $$
其中:
$$ \omega_n = e^{2\pi i/n} $$
是单位圆上的 n 个等分点,也称为“单位根”(roots of unity)。
3.1. 单位根(De Moivre 数)
$\omega_n$ 及其幂次构成了傅里叶变换的基础。虽然 $\omega_n$ 可以表示为三角函数形式,但使用指数形式 $e^{2\pi i/n}$ 更有助于理解其性质。
以 $n=8$ 为例,$\omega_8$ 是第一个单位根。下图展示了 8 个单位根,其中第一个根 $\omega_8$ 与 x 轴夹角为 45°,即 $e^{\frac{i\pi}{4}}$,后续的根则是其更高次幂:
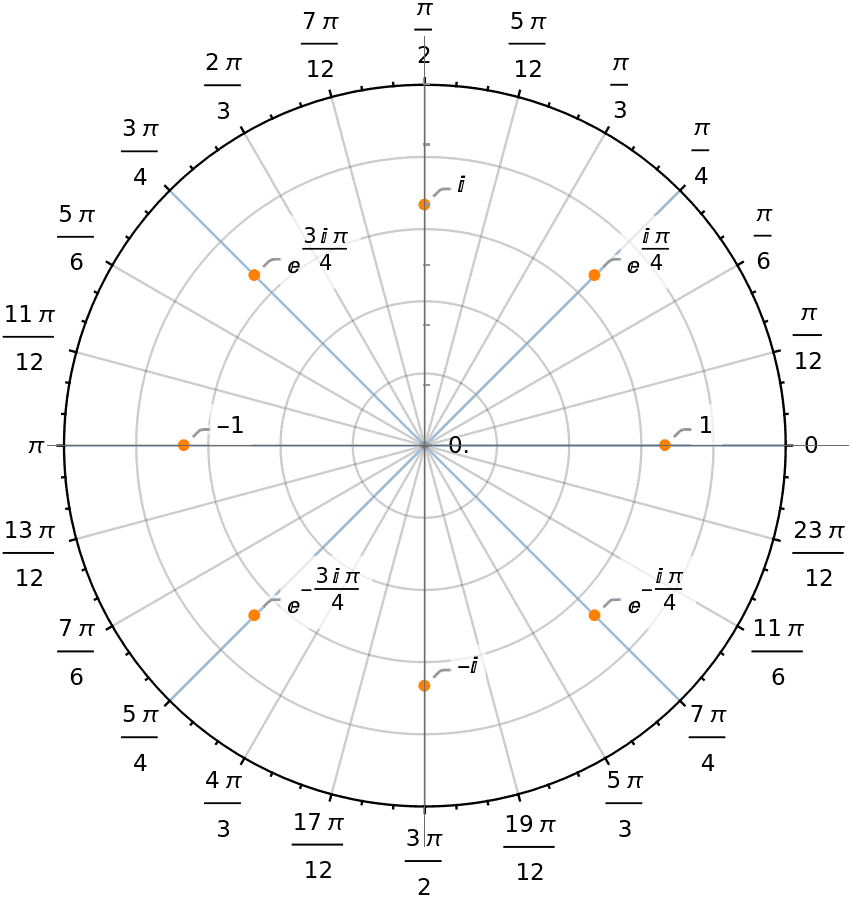
我们可以将 $\omega_n^j$ 与输入序列相乘理解为:每个单位根“感知”输入序列中的某个频率分量。当单位根数量足够多时,它们的加权和可以逼近原始输入序列。
如下动图展示了随着单位根数量增加,傅里叶级数逐渐逼近原始函数的过程:
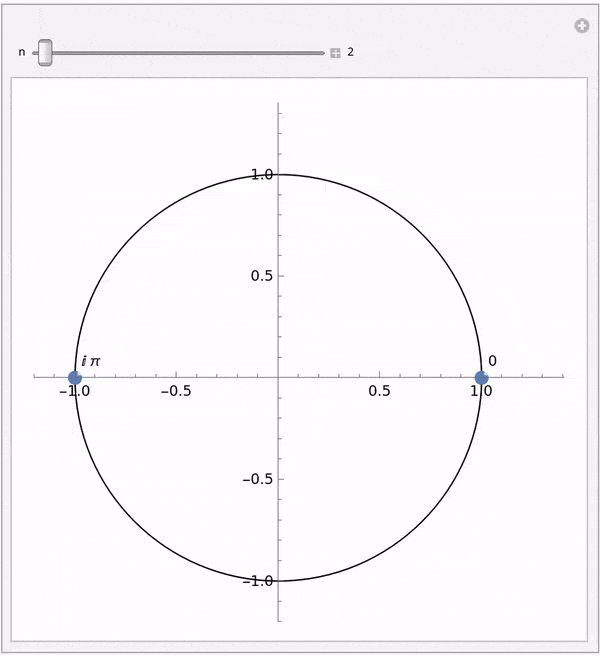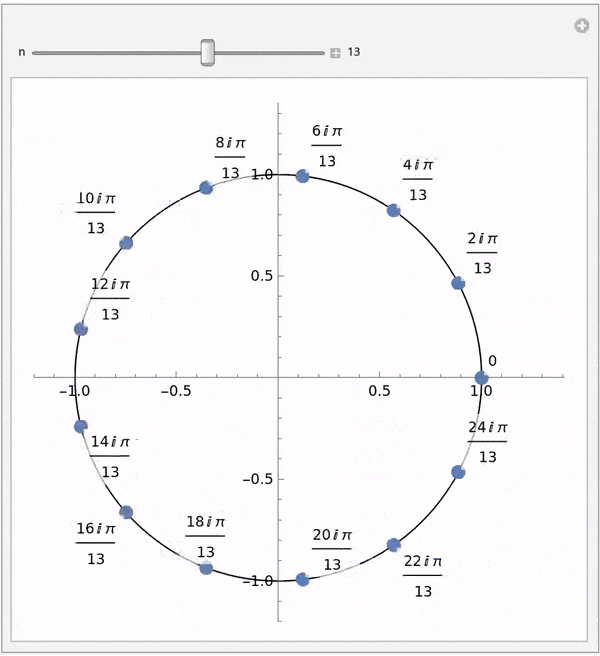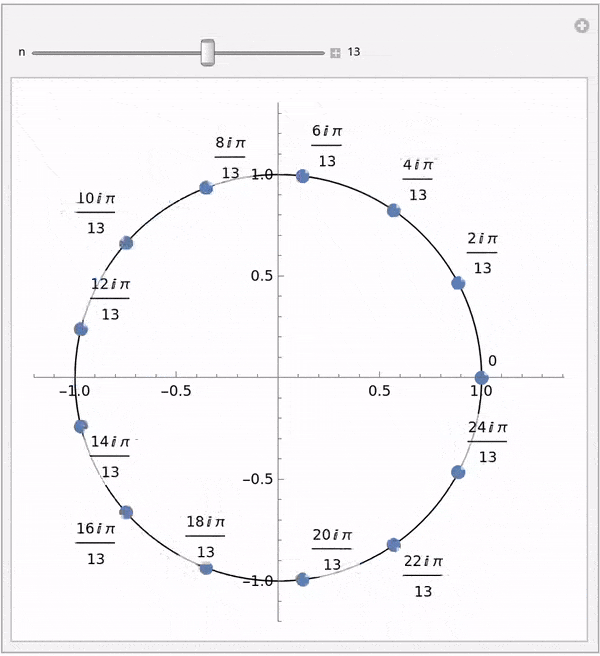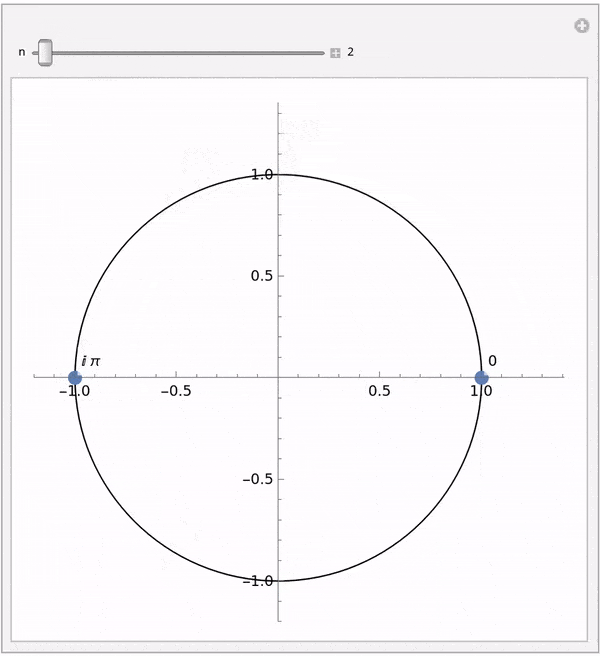
每计算一个 $A_i$,需要 n 次复数乘法和 n-1 次复数加法。因此,整个 DFT 的时间复杂度为 $O(n^2)$,即 $n^2$ 次复数乘法和 $n^2 - n$ 次复数加法。
4. 快速傅里叶变换(FFT)
Cooley 和 Tukey 提出的关键观察是:如果 n 是合数(即 n = n₁ × n₂),则可以通过分解 DFT 来显著降低计算复杂度。
例如,当 $n=8$ 时,$(\omega_8)^2 = \omega_4$,即平方后得到的单位根对应于 n=4 的单位根。这种特性使得我们可以将一个大的 DFT 分解为多个小的 DFT。
4.1. DFT 向量表示法
为了便于理解,我们可以将 DFT 表示为矩阵形式:
$$ \mathbf{A} = F(n) \cdot \mathbf{a} $$
其中,$F(n)$ 是一个 n×n 的矩阵,其元素为 $\omega^{ij}$,例如当 n=4 时:
$$ F(4) = \begin{bmatrix} 1 & 1 & 1 & 1 \ 1 & \omega & \omega^2 & \omega^3 \ 1 & \omega^2 & \omega^4 & \omega^6 \ 1 & \omega^3 & \omega^6 & \omega^9 \end{bmatrix} $$
直接计算这个矩阵与输入向量的乘积需要 $n^2$ 次复数运算。但我们可以利用单位根的重复性和对称性来优化这个过程。
4.2. 复杂度优化思路
FFT 的核心思想是通过递归地将 DFT 分解为两个较小的 DFT(分别处理偶数索引和奇数索引),从而将复杂度从 $O(n^2)$ 降低到 $O(n \log n)$。
例如,我们可以将 $F(4)$ 分解为两个 $F(2)$ 矩阵的组合,并引入一个排列矩阵来将奇偶索引分开:
$$ F(4) = \begin{bmatrix} I_2 & D_2 \ I_2 & -D_2 \end{bmatrix} \cdot \begin{bmatrix} F(2) & 0 \ 0 & F(2) \end{bmatrix} \cdot \text{排列矩阵} $$
其中 $D_2$ 是一个对角矩阵,其对角线元素为 $(1, \omega)$。
4.3. 引入“修正矩阵”
为了将分解后的子矩阵正确组合成原始的 DFT 结果,我们引入一个修正矩阵(Fix-up Matrix):
$$ \begin{bmatrix} I_n & D_n \ I_n & -D_n \end{bmatrix} $$
这个矩阵负责将两个子 DFT 的结果合并为一个完整的 DFT。通过递归应用这一过程,我们可以将 DFT 分解为 log₂n 层,每一层只需 O(n) 次操作,最终复杂度为 $O(n \log n)$。
✅ 举例说明:
- 对于 $n=1024$,标准 DFT 需要 $1024^2 = 1,048,576$ 次复数乘法。
- 使用 FFT 后,仅需 $ \frac{1}{2} \cdot 1024 \cdot \log_2(1024) = 5120 $ 次复数乘法。
⚠️ 注意:若 n 不是 2 的幂次,可以通过补零(padding)将其扩展为最近的 2 的幂次长度。
5. 应用场景
傅里叶变换在众多领域中都有广泛应用。我们选取两个典型场景进行说明。
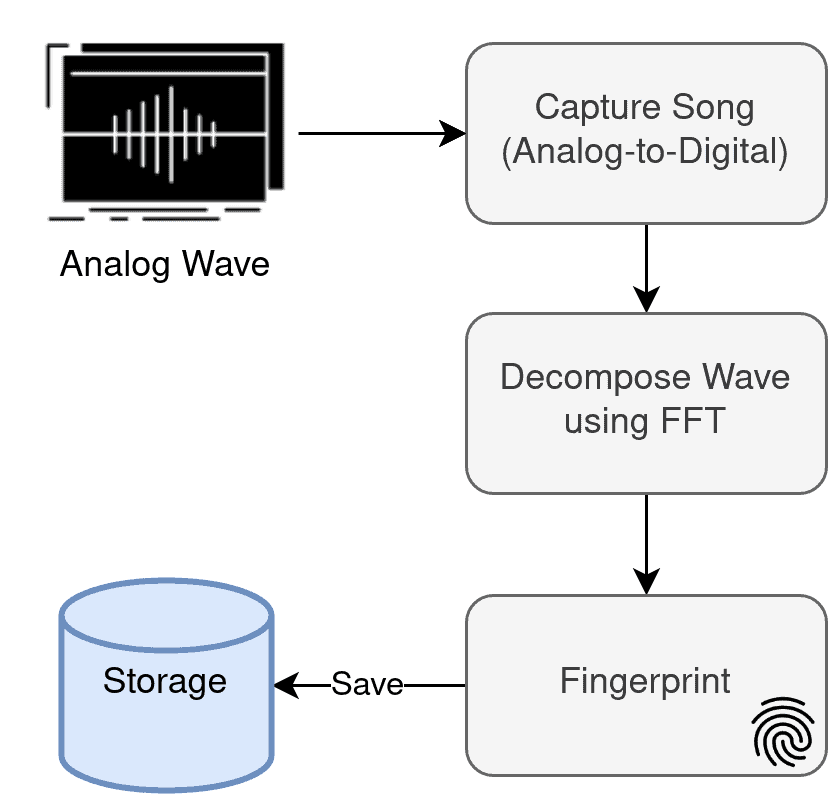
5.1. 音频识别(如 Shazam)
Shazam 能在几秒钟内识别出一首歌曲,其核心流程如下:
- 录音并将其转换为数字信号(模拟转数字)
- 使用 FFT 将时域信号转换为频域表示
- 提取频谱指纹(Fingerprint)
- 与数据库中的歌曲指纹进行比对
下图展示了 Shazam 识别歌曲的流程示意:
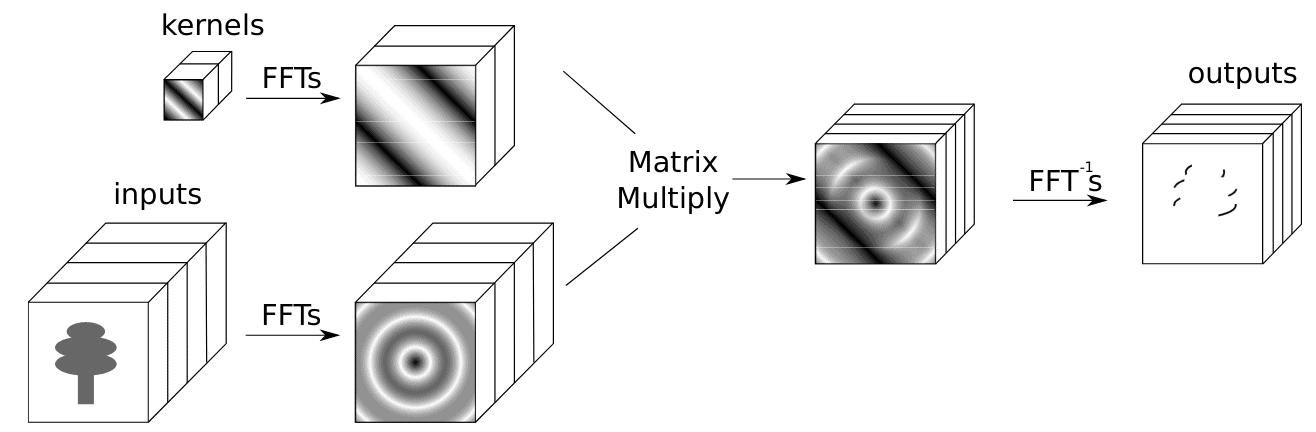
5.2. 卷积定理
卷积定理指出:时域中的循环卷积等价于频域中的逐点乘法。
设 $\mathcal{F}$ 表示傅里叶变换,$\mathcal{F}^{-1}$ 表示其逆变换,则函数 $f$ 与 $g$ 的卷积可表示为:
$$ f * g = \mathcal{F}^{-1}\left{ \mathcal{F}{f} \cdot \mathcal{F}{g} \right} $$
传统卷积计算复杂度为 $O(n^2k^2)$,而基于 FFT 的方法可将复杂度降至 $O(n^2 \log n)$。
✅ 典型应用包括:
- 图像处理(如边缘检测)
- 光学图像复原(锐化模糊照片)
- 卷积神经网络(CNNs)
下图展示了传统卷积与 FFT 卷积在运算量上的对比:
6. 总结
本文从数学角度简要介绍了快速傅里叶变换(FFT)的基本原理,并说明了其在音频识别、图像处理等领域的广泛应用。
虽然傅里叶变换的思想早在两个世纪前就已提出,但直到 Cooley 和 Tukey 提出 FFT 算法后,它才真正走进大规模应用。FFT 的出现不仅提升了信号处理的效率,也成为现代数字信号处理和人工智能技术的基石之一。