Gale-Shapley Algorithm

1. Introduction

In this article, we’ll learn what the stable matching problem is, and how the Gale-Shapley algorithm can solve it efficiently.

2. The Stable Matching Problem

We start with two sets of equal size – and . Every element in set has an ordered list of preferences for matching with elements in set , and the same is true in the opposite direction.

The stable matching problem is the problem of finding a stable set of matches between all elements in these sets. Stable in this sense means that, for every match between elements ​ and ​, there is no alternative match that would prefer over , and for which would also prefer over its own current match.

If this holds for all elements in both sets, then the match between the two sets is considered stable.

In other words, there is no pair of elements who would both mutually prefer each other over their current matches.

2.1. Real-World Examples

This problem seems hypothetical, but there are a number of important applications for it, including:

• Medical residency matching – assigning medical students to hospital appointments.
• University admissions – matching students to available university places.
• Load balancing – assigning users to servers in distributed internet services.
• Organ donation – matching organ donors to recipients.
• And many more.

All of these are real-world cases where this exact problem arises and an efficient solution is needed.

3. The Gale-Shapley Algorithm

The Gale-Shapley algorithm is a way to find a stable solution to this problem. In particular, it also finds an optimal solution for the first set. That is, a solution where every member of the first set has been matched with their best possible partner.

In order to start, we need to have every member of each set and their ordered list of preferences. The algorithm is then as follows:

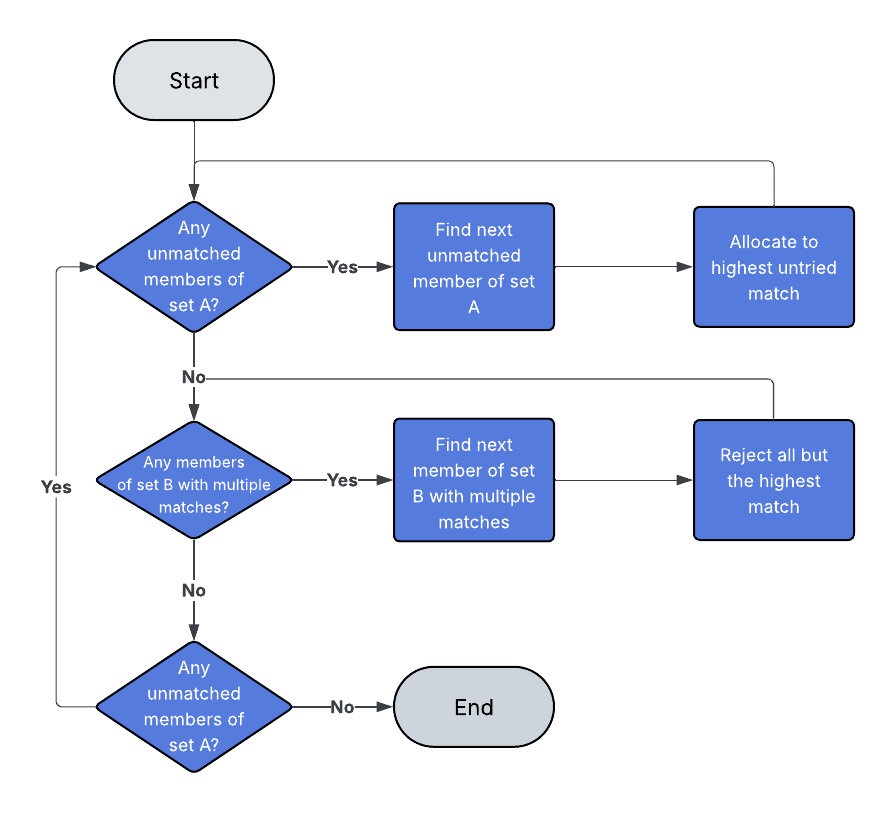
Here, we are iterating over every unmatched member of our first set and assigning them to their highest preference from the second set that they haven’t yet tried. Each member of the second set will then accept the match that is their highest preference, rejecting any others. These rejected members are then considered to be unmatched for now. This then repeats until we have matched all of our members.

We can express this in pseudocode as follows:

algorithm GaleShapley(setA, setB, preferencesA, preferencesB)
// INPUT
//   setA = The first set of elements to match
//   setB = The second set of elements to match
//   preferencesA = Dictionary where the keys are elements in setA and the values are an ordered list of elements in setB
//   preferencesB = Dictionary where the keys are elements in setB and the values are an ordered list of elements in setA
// OUTPUT
//   The mapping between elements in setA and setB

  result := {}
  unmatchedA := setA
  
  while (unmatchedA.notEmpty())
    for (elementA in unmatchedA)
      elementB := preferencesA[elementA].shift() // Shift pops off the front of the list.

      if (elementB == null)
        // No more matches possible for elementA
        unmatchedA.remove(elementA)
      else
        previousMatch := result[elementB]
        if (previousMatch == null)
          // There was no previous match
          result[elementB] = elementA
          unmatchedA.remove(elementA)
        else
          // There was a previous match, so see which is preferred
          newMatchPreference := preferencesB[elementB].indexOf(elementA)
          previousMatchPreference := preferencesB[elementB].indexOf(previousMatch)
          if (newMatchPreference < previousMatchPreference)
            // The new match is preferred over the old one
            result[elementB] = elementA
            unmatchedA.remove(elementA)
            unmatchedA.add(previousMatch)
  return result

Note that we compare the matches one at a time, rather than collecting all matches first and then comparing. This produces the same result but with less storage required.

3.1. Complexity

Since the algorithm involves repeatedly iterating over all of the unmatched elements, this will have time complexity of at worst. However, this is only achieved if every member of the first set ends up matching with their last preference since that will then mean that we’re processing every possible set of matches.

In addition, this algorithm will have space complexity of since we only need to store the current match for any element.

4. Worked Example

To demonstrate how this works, we’ll match up 4 medical students – , , and – and 4 hospital spaces – , , and .

Each of the medical students has the following preferences for hospitals:

Student

First Preference

Second Preference

Third Preference

Fourth Preference

Each of the hospitals then has the following preferences for students:

Hospital

First Preference

Second Preference

Third Preference

Fourth Preference

We need to match these two sets together.

For the first iteration, we’ll match each student to their top preference:

• and match with . matches with and is rejected.
• matches with
• matches with

At this point, we have matches , and . We don’t have matches for all of the students, so we try again:

• matches with .
• was already matched with , but prefers so is rejected.

We now have matches , and . We still don’t have matches for all of the students, so we try again:

• matches with
• was already matched with , and prefers so is rejected.

The matches haven’t changed here, so we keep going:

• matches with but is rejected because prefers it’s current match.
• matches with and is accepted.

At this point, all of the students have been matched and the result is stable.

• is matched with
• is matched with
• is matched with
• is matched with

We now know that this gives the best results for matching these sets and that all of the students have got the best possible placement given the competing preferences.

5. Conclusion

Here we’ve looked into the stable matching problem, and we’ve seen the Gale-Shapley algorithm for finding optimal matches between two sets. Next time you need to match two sets together, why not give it a try?