1. 概述
在本教程中,我们将介绍图(Graph)这种数据结构的基本概念,并探讨它在 Java 中的具体实现方式、常见操作,以及可用于图处理的主流 Java 库。
图是一种用于表示相互连接的数据结构,例如社交网络中用户之间的关系。
2. 图数据结构
图由顶点(Vertex)和边(Edge)组成。
- 顶点表示实体(例如人)
- 边表示实体之间的关系(例如朋友关系)
我们来看一个简单的图示例:
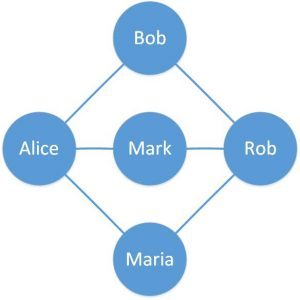
这是一个包含五个顶点和六条边的无向图。圆圈代表人,连线代表他们在某个在线平台上的好友关系。
根据边的不同属性,图可以分为以下几种类型,我们将在后续章节简要介绍。但为了保持代码示例简洁,本文将主要围绕“简单无权无向图”展开。
2.1. 有向图
如果图中的边具有方向性,则该图为有向图(Directed Graph)。
例如,可以用来表示谁发出了好友请求:
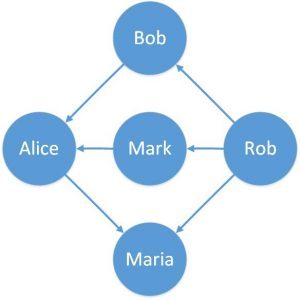
可以看到,图中每条边都有明确的方向。有些边可能是双向的。
2.2. 带权图
如果图中的边带有权重(Weight),则称为带权图(Weighted Graph)。
比如可以表示好友关系建立的时间长短:
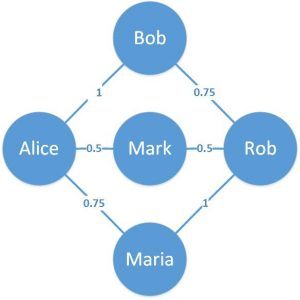
可以看到,每条边上都标注了数值,表示关系的强度或时间。
3. 图的表示方式
图可以用多种方式表示,常见的包括邻接矩阵(Adjacency Matrix)和邻接表(Adjacency List)。两者各有优劣。
3.1. 邻接矩阵
邻接矩阵是一个大小为 V×V 的二维数组(V 是顶点数)。
- 矩阵元素值为 1 表示两个顶点之间存在边
- 值为 0 表示无边
以我们前面的图为例,其邻接矩阵如下:
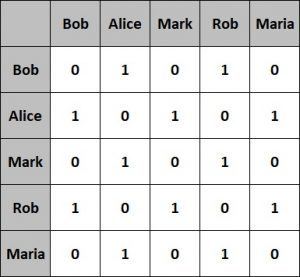
✅ 优点:查询两个顶点是否相连非常高效
❌ 缺点:空间占用较大,尤其是稀疏图时浪费严重
3.2. 邻接表
邻接表是一个数组,每个元素是一个链表(或集合),记录与该顶点相邻的所有顶点。
同样以前面的图为例:
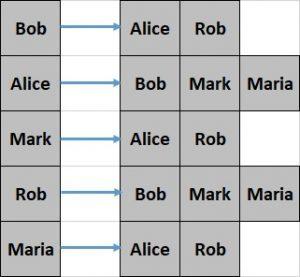
✅ 优点:节省空间,适合稀疏图
❌ 缺点:查询两个顶点是否相连不如邻接矩阵快
在本教程中,我们将使用邻接表来实现图结构。
4. Java 中的图实现
Java 标准库中没有内置的图结构,但我们可以通过 Java Collections 来实现。
首先定义一个顶点类:
class Vertex {
String label;
Vertex(String label) {
this.label = label;
}
// equals and hashCode
}
⚠️ 注意:为了配合 Java 集合框架(如 Map、Set),必须重写 equals() 和 hashCode() 方法。
接着定义图类,使用邻接表结构:
class Graph {
private Map<Vertex, List<Vertex>> adjVertices;
// standard constructor, getters, setters
}
图本质上就是一组顶点和边的集合,我们可以通过 Java 的 Map 来表示邻接表。
5. 图的变更操作
我们来实现图的基本操作,包括添加/删除顶点和边。
添加/删除顶点
void addVertex(String label) {
adjVertices.putIfAbsent(new Vertex(label), new ArrayList<>());
}
void removeVertex(String label) {
Vertex v = new Vertex(label);
adjVertices.values().stream().forEach(e -> e.remove(v));
adjVertices.remove(new Vertex(label));
}
添加/删除边
void addEdge(String label1, String label2) {
Vertex v1 = new Vertex(label1);
Vertex v2 = new Vertex(label2);
adjVertices.get(v1).add(v2);
adjVertices.get(v2).add(v1);
}
void removeEdge(String label1, String label2) {
Vertex v1 = new Vertex(label1);
Vertex v2 = new Vertex(label2);
List<Vertex> eV1 = adjVertices.get(v1);
List<Vertex> eV2 = adjVertices.get(v2);
if (eV1 != null)
eV1.remove(v2);
if (eV2 != null)
eV2.remove(v1);
}
构建图示例
Graph createGraph() {
Graph graph = new Graph();
graph.addVertex("Bob");
graph.addVertex("Alice");
graph.addVertex("Mark");
graph.addVertex("Rob");
graph.addVertex("Maria");
graph.addEdge("Bob", "Alice");
graph.addEdge("Bob", "Rob");
graph.addEdge("Alice", "Mark");
graph.addEdge("Rob", "Mark");
graph.addEdge("Alice", "Maria");
graph.addEdge("Rob", "Maria");
return graph;
}
获取相邻顶点
List<Vertex> getAdjVertices(String label) {
return adjVertices.get(new Vertex(label));
}
6. 图的遍历
图的遍历是很多图算法的基础,常见的有深度优先遍历(DFS)和广度优先遍历(BFS)。
6.1. 深度优先遍历(DFS)
深度优先遍历会沿着一条路径尽可能深入,然后再回溯。
Set<String> depthFirstTraversal(Graph graph, String root) {
Set<String> visited = new LinkedHashSet<String>();
Stack<String> stack = new Stack<String>();
stack.push(root);
while (!stack.isEmpty()) {
String vertex = stack.pop();
if (!visited.contains(vertex)) {
visited.add(vertex);
for (Vertex v : graph.getAdjVertices(vertex)) {
stack.push(v.label);
}
}
}
return visited;
}
✅ 使用栈(Stack)实现
🧪 示例测试:
@Test
public void givenAGraph_whenTraversingDepthFirst_thenExpectedResult() {
Graph graph = createGraph();
assertEquals("[Bob, Rob, Maria, Alice, Mark]",
GraphTraversal.depthFirstTraversal(graph, "Bob").toString());
}
6.2. 广度优先遍历(BFS)
广度优先遍历会先访问当前层的所有顶点,再进入下一层。
Set<String> breadthFirstTraversal(Graph graph, String root) {
Set<String> visited = new LinkedHashSet<String>();
Queue<String> queue = new LinkedList<String>();
queue.add(root);
visited.add(root);
while (!queue.isEmpty()) {
String vertex = queue.poll();
for (Vertex v : graph.getAdjVertices(vertex)) {
if (!visited.contains(v.label)) {
visited.add(v.label);
queue.add(v.label);
}
}
}
return visited;
}
✅ 使用队列(Queue)实现
🧪 示例测试:
@Test
public void givenAGraph_whenTraversingBreadthFirst_thenExpectedResult() {
Graph graph = createGraph();
assertEquals("[Bob, Alice, Rob, Mark, Maria]",
GraphTraversal.breadthFirstTraversal(graph, "Bob").toString());
}
7. 初始化与打印图
我们可以编写一个简单的 Java 应用来初始化并打印图结构:
static Graph createGraph() {
Graph graph = new Graph();
graph.addVertex("Bob");
graph.addVertex("Alice");
graph.addVertex("Mark");
graph.addVertex("Rob");
graph.addVertex("Maria");
graph.addEdge("Bob", "Maria");
graph.addEdge("Bob", "Mark");
graph.addEdge("Maria", "Alice");
graph.addEdge("Mark", "Alice");
graph.addEdge("Maria", "Rob");
graph.addEdge("Mark", "Rob");
return graph;
}
public static void main(String[] args) {
Graph graph = createGraph();
Set result = GraphTraversal.breadthFirstTraversal(graph, "Bob");
System.out.println(result.toString());
}
输出结果:
[Bob, Maria, Mark, Alice, Rob]
8. Java 图处理库
在实际开发中,我们并不总是需要从零实现图结构。以下是一些优秀的 Java 图处理库:
8.1. JGraphT
JGraphT 是 Java 中最流行的图处理库之一,支持创建简单图、有向图、带权图等,并提供大量图算法实现。
8.2. Google Guava
Google Guava 提供了 Graph、ValueGraph 和 Network 接口,支持可变和不可变图。
8.3. Apache Commons Graph
Apache Commons Graph 是 Apache 提供的图结构工具包,支持常见图算法。
8.4. JUNG
Java Universal Network/Graph (JUNG) 是一个功能强大的图建模与可视化框架,支持聚类、分解、优化等算法。
这些库不仅提供图结构的实现,还支持更高级的图处理框架,例如:
- Apache Giraph:Facebook 用于分析用户图结构
- Apache TinkerPop:常用于图数据库之上
9. 总结
在本文中,我们介绍了图的基本概念、表示方式,并用 Java 实现了简单的图结构。我们还演示了图的遍历方法(DFS 和 BFS),并介绍了常用的图处理库。
图结构是很多高级算法和系统的基础,掌握它的实现与应用对 Java 开发者来说非常重要。