Is log(n!) of the Same Order as n log(n)?

1. Introduction

In this tutorial, we’ll discuss the asymptotic properties of $\log n!$ .

An example of an algorithm whose time complexity corresponds to this function is binary search over permutations of an array.

2. Complexity

We define the complexity class of an algorithm by analyzing how the number of steps it performs increases with the input size.

Technically, a step in an algorithm can be any operation it performs. Although we can focus only on specific ones, such as arithmetic or IO operations, we usually assume that all atomic operations are of the same order, so we count them all. That way, we get a non-negative function mapping an integer n > 0 to the number of steps our algorithm performs given the input of size .

The asymptotic notation distinguishes between several cases.

Big O denotes asymptotic upper bounds. We say that is an asymptotic upper bound of (denoted as $f \in O(g)$ ) if there’s a constant and an input size n_0 such that for all larger inputs $n \geq n_0$ , we have $f(n) \leq k g(n)$ .

Big Omega defines asymptotic lower bounds. We say that is an asymptotic lower bound of (and write $f \in \Omega(g)$ ) if there’s a constant and an input size n_o such that for all larger inputs $n \geq n_0$ , we have $f(n) \geq k g(n)$ .

Finally, we say that $\boldsymbol{f}$ is of the same order as $\boldsymbol{g}$ (and write $\boldsymbol{f \in \Theta(g)}$ ) if $\boldsymbol{f}$ is asymptotically bounded by $\boldsymbol{g}$ from below and above at the same time:

$[f \in \Theta(g) \iff f \in O(g) \land f \in \Omega(g)]$

3. The Upper Bound

Let’s note that for every input size $n \geq 1$ , it holds:

$[(1 \leq n) \land (2 \leq n) \land \ldots \land (n \leq n)]$

From there:

$[\begin{aligned} n! &= \left( n \times (n-1) \times \ldots \times 2 \times 1 \right) \\ &\leq \underbrace{n \times n \times \ldots n \times n }_{n \text{ times}} \\ &= n^n \end{aligned}]$

Taking the logarithms of both sides, we get:

$[n! \leq n^n \implies \log n! \leq \log (n^n) = n \log n]$

To formally prove that $\log n! \in O(n \log n)$ , we need to show that there exists n_0 and such that:

$[\log n! \leq k \times (n \log n) \qquad \text{ for all } n\geq n_0]$

Our derivation shows $\boldsymbol{\log n! \leq n \log n}$ for every $n \geq 1$ , so n_0=1 and k=1 .

3.1. Does the Base of the Logarithm Matter?

Since the logarithmic function is strictly increasing when the base is greater than 1, taking the logarithms of both sides of $n! \leq n^n$ will preserve the relation $\leq$ if we use a base > 1 .

These are bases we consider in algorithmic analysis, so we don’t have to be concerned with a fractional base.

4. The Lower Bound

First, let’s note that for any $n \in N$ , we have:

$[\begin{aligned} n! &= n \times (n-1) \times (n-2) \times \ldots \times 2 \times 1 \\ &= n \times (n-1) \times (n-2) \times \ldots \times \lceil n/2 \rceil \times \ldots \times 2 \times 1 \\ &\geq n \times (n-1) \times (n-2) \times \ldots \times \lceil n/2 \rceil \end{aligned}]$

Now, let’s use the fact that all these numbers $n, n-1, \ldots,\lceil n/2 \rceil$ are greater than or equal to n/2 :

$[\begin{aligned} n! &\geq n \times (n-1) \times (n-2) \times \ldots \times \lceil n/2 \rceil \\ &\geq \underbrace{\frac{n}{2} \times \frac{n}{2} \times \ldots \times \frac{n}{2}}_{n - \lceil n/2 \rceil + 1 \text{ times}} \\ &=\left( \frac{n}{2} \right)^{n - \lceil n/2 \rceil + 1} \end{aligned}]$

Since $\lceil n/2 \rceil \leq n/2+1$ , we have:

$[n - \lceil n/2 \rceil + 1 \geq n - n/2 -1 + 1 = n/2]$

Therefore:

$[n! \geq \left( \frac{n}{2} \right)^{\frac{n}{2}}]$

Let’s take logarithms:

$[\begin{aligned} \log n! &\geq \log \left( \left( \frac{n}{2} \right)^{\frac{n}{2}} \right) \\ &=\frac{n}{2} \log \frac{n}{2} \\ &= \frac{n}{2} (\log n - \log 2) \\ &\geq \frac{1}{2} n\log n \end{aligned}]$

Setting $k=\frac{1}{2}$ and n_0=1 , we get that:

$[\log n! \in \Omega(n \log n)]$

The proof was longer than for $\log n! \in O(n \log n)$ because, to make it rigorous, we had to use $\lceil n/2 \rceil$ . As is the case for Big O, the base of the logarithm doesn’t matter.

5. The Asymptotic Order and Equivalence

Since we have:

$[\log n! \in O(n \log n) \text{ and } \log n! \in \Omega(n \log n)]$

we can conclude that $\boldsymbol{\log n! \in \Theta(n \log n)}$ . So, $\log n!$ is of the same order as $n \log n$ .

5.1. Asymptotic Equivalence

However, are these two functions asymptotically equivalent? The relation of asymptotic equivalence $\boldsymbol{\sim}$ is similar to $\boldsymbol{\Theta}$ but has a stronger condition:

$[f(n) \sim g(n) \iff (\forall \varepsilon >0)(\exists n_0 \in N)(\forall n \geq n_0) \left| \frac{f(n)}{g(n)} - 1 \right| < \varepsilon]$

For $f \in \Theta(g)$ , we must have $k_1 g(n) \leq f(n) \leq k_2 g(n)$ starting from some n = n_0 . For $f(n) \sim g(n)$ , it should hold that f(n) and g(n) are approximately the same in the limit. In other words:

$[f(n) \sim g(n) \iff \lim_{n \rightarrow \infty} \frac{f(n)}{g(n)} = 1]$

5.2. Is log n! ~ n log n?

Let’s compute the limit:

$[\begin{aligned} \lim_{n \rightarrow \infty} \frac{\log n!}{n \log n} &= \lim_{n \rightarrow \infty} \frac{\log \left( n \times (n-1) \times \ldots \times 2 \times 1 \right)}{n \log n} \\ &= \lim_{n \rightarrow \infty} \frac{\sum_{k=1}^{n} \log k}{n \log n} \\ &= \lim_{n \rightarrow \infty} \sum_{k=1}^{n} \frac{\log k}{n \log n} \end{aligned}]$

Since every $k \leq n$ , we can substitute $\log k$ for $\log n$ :

$[\sum_{k=1}^{n} \frac{\log k}{n \log n} \leq \sum_{k=1}^{n} \frac{\log n}{n \log n} = \frac{n \log n}{n \log n} = 1]$

This way, we get the upper bound.

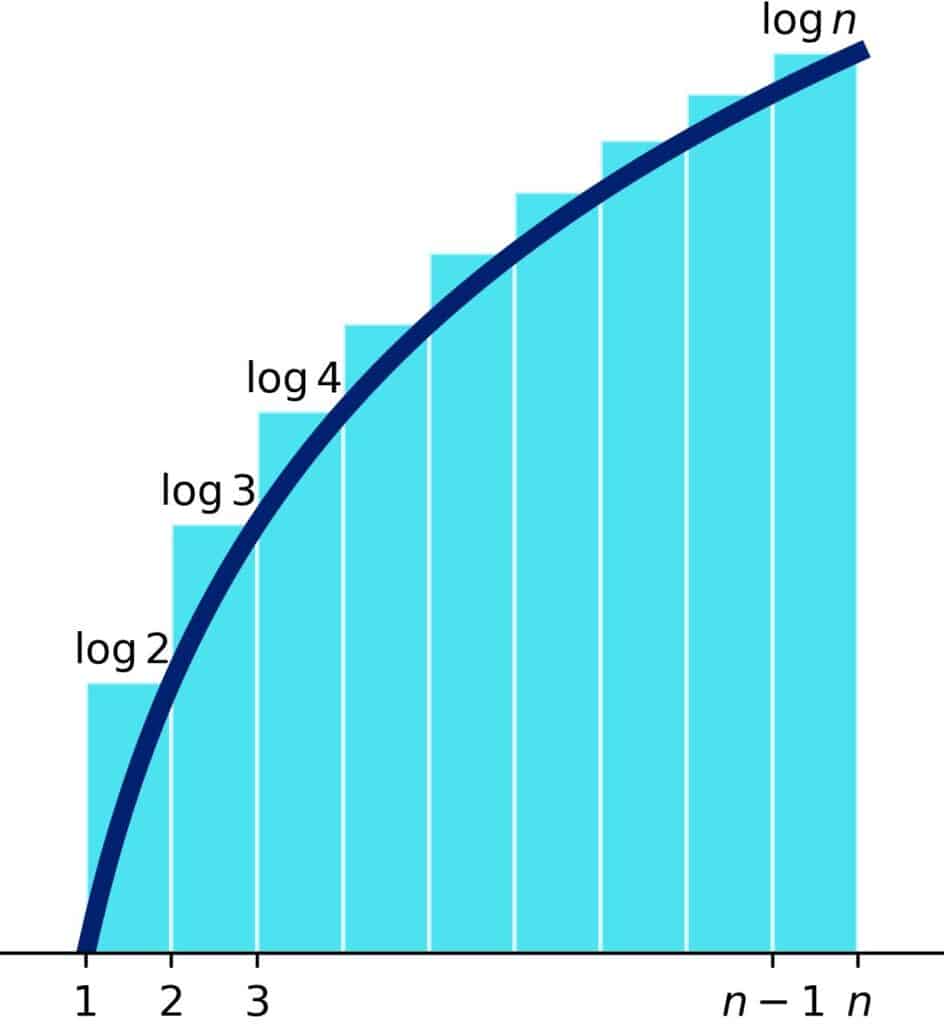
To compute the lower bound, let’s inspect the following plot:

The shaded area equals the sum $\sum_{k=2}^n \log k$ . It overestimates the area under $\log x$ between x=1 and x=n :

$[\int_{1}^{n} \log x dx \leq \sum_{k=2}^{n} \log k]$

Since $\log 1=0$ , we can add it to both sides to get:

$[\int_{1}^{n} \log x dx \leq \sum_{k=1}^{n}\log k = \log n!]$

For any base a>0 , we can integrate by parts to get:

$[\int_{1}^{n} \log_a x dx = \frac{1}{\ln a}(n \ln n - n + 1)]$

So:

$[\begin{aligned} \frac{1}{\ln a}(n \ln n - n + 1) &\leq \log_a n! \\ \frac{\frac{1}{\ln a}(n \ln n - n + 1)}{n \log_a n} &\leq \frac{\log_a n!}{n \log_a n} \\ \frac{\frac{1}{\ln a}(n \ln n - n + 1)}{n \frac{\ln n}{\ln a}} &\leq \frac{\log_a n!}{n \log_a n} \\ \frac{n \ln n - n + 1}{n \ln n} &\leq \frac{\log_a n!}{n \log_a n} \end{aligned}]$

As $n \rightarrow \infty$ , the lower bound approaches 1. Therefore, we have:

$[n \rightarrow 1 \implies 1 \leq \frac{\log n!}{ n \log n} \leq 1]$

That means that the limit is also one:

$[\lim_{n \rightarrow \infty}\frac{\log n!}{n \log n} = 1]$

So, it also holds that $\boldsymbol{\log n! \sim n \log n}$ .

6. Stirling’s Approximation

Stirling’s approximation of $\ln n!$ (and ) can be derived by approximating the integral of $\ln x$ over [1, n] . The formula is:

$[\ln n! = n \ln n - n + O(\ln n)]$

This means that the error of approximating $\ln n!$ with $n \ln n - n$ is $O(\ln n)$ , i.e., it’s asymptotically bounded by $\ln n$ . Since the base doesn’t affect the asymptotic behavior, we have:

$[\log n! = n \log n - n + O(\log n) \implies \log n! \sim n \log n]$

It can be shown that this approximation can be restated as:

$[n! \sim \sqrt{2 \pi n} \left( \frac{n}{e} \right)^n]$

Stirling’s approximation immediately reveals the asymptotic relation between $\log n!$ and $n \log n$ , but its proof deals with mathematical details that are out of the scope of this article.

7. Conclusion

In this article, we analyzed the asymptotic properties of $\log n!$ . This function determines the complexity of algorithms searching permutation spaces similarly to binary search.

The function $\log n!$ is of the same asymptotic order as and is asymptotically equivalent to $n \log n$ .

Persistence

REST

Security