1. 引言
从 1970 年代到 1990 年代的汽车设计来看,最大的变化莫过于车身线条的转变。70 年代的车方正,90 年代的车则更加流线型。这种变化不仅提升了美感,也提高了燃油效率。
在上世纪 60 年代,美国汽油便宜,但在欧洲,油价一直较高。1962 年,雷诺汽车的工程师皮埃尔·贝塞尔(Pierre Bézier)和雪铁龙的数学家保罗·德·卡斯特廖(Paul de Casteljau)分别开发了贝塞尔曲线,用于拟合光滑的曲线和曲面,从而实现更流线型的车身设计并提升燃油效率。
在本教程中,我们将探讨分段多项式插值背后的数学原理,并了解一些有趣的曲线构造方法。
2. 从点或向量的角度理解多项式
多项式是科学和数学中基本的逼近工具。我们先来回顾一下对多项式的理解。一个 n 次多项式本质上是一个函数,它接受一个实数 x 作为输入,并映射到另一个实数 y = p(x),其中:
$$ p(x) = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0 $$
在数学中,多项式是一种特殊的对象——它们是多项式空间 $\mathcal{P}_n$ 中的向量。
我们可以这样理解:想象向量,通常会想到大学物理课上的箭头向量。这完全没问题!
我们知道,三维空间中的任意向量 $\vec{v} = (v_x, v_y, v_z)$ 都可以表示为基向量 $\hat{i} = (1, 0, 0)$、$\hat{j} = (0, 1, 0)$、$\hat{k} = (0, 0, 1)$ 的线性组合。向量加法是按分量进行的,标量乘法也是如此。
再来看所有次数不超过 2 的多项式构成的集合:
$$ \mathcal{P}_2 = {a_2 x^2 + a_1 x + a_0 : a_j \in \mathbb{R}, j = 0,1,2} $$
$\mathcal{P}_2$ 中的多项式与三维空间中的几何向量是同构的。任意一个 2 次多项式都可以表示为基多项式 1、x 和 $x^2$ 的线性组合。这些基多项式相当于单位向量:
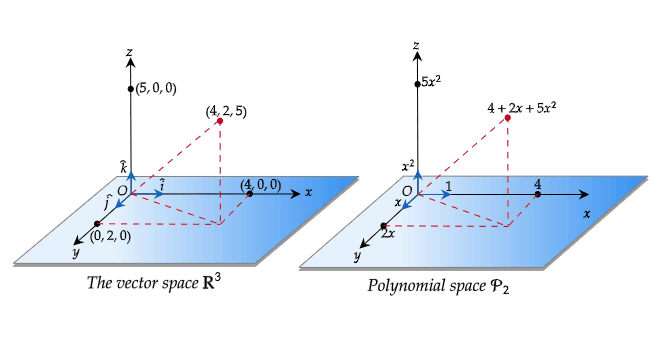
就像我们可以为三维空间选择不同的基向量一样,我们也可以为多项式空间 $\mathcal{P}_2$ 选择不同的基。例如:
$$ 1 - 2x + x^2,\quad 0 + 2x - 2x^2,\quad 0 + 0x + x^2 $$
也是 $\mathcal{P}_2$ 的一组基。例如,任意一个多项式如 $4 + 2x + 5x^2$ 可以表示为这些基的线性组合:
$$ 4 + 2x + 5x^2 = 4(1 - 2x + x^2) + 5(0 + 2x - 2x^2) + 11(0 + 0x + x^2) $$
3. 分段多项式插值的必要性
回顾一下多项式插值的问题:我们有一个未知函数 f,它在区间 [a, b] 上的值未知,但已知在一些点 $(x_0, y_0), (x_1, y_1), \ldots, (x_n, y_n)$ 上的值。我们希望通过一个多项式 p(x) 来逼近这个函数。
我们知道,n+1 个点可以唯一确定一个 n 次多项式。但当数据点增多时,使用单一高次多项式插值会出现剧烈震荡,尤其是在端点附近。这就是著名的 Runge 现象。
解决这个问题的方法之一是使用 分段多项式插值,即把整个区间划分为若干段,每段使用低次多项式进行插值。
3.1 Runge 现象示例
考虑函数 $f(x) = 1/(1 + 25x^2)$ 在 [-1, 1] 区间上使用 11 个等距点插值。使用单一 10 次多项式插值时,曲线在端点附近剧烈震荡:
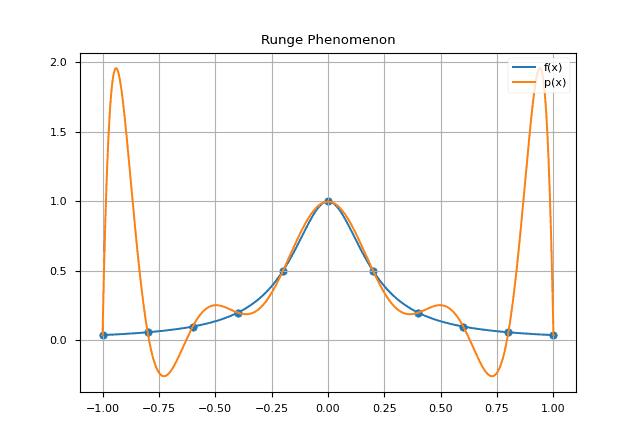
而使用分段插值则可以避免这一问题。
4. Bernstein 多项式与贝塞尔曲线
贝塞尔曲线在计算机图形学中无处不在。其基本思想如下:
考虑一个航天器从点 $p_0 = (x_0, y_0)$ 直线运动到 $p_1 = (x_1, y_1)$,时间 t ∈ [0, 1]。其位置为:
$$ p(t) = (1 - t)p_0 + t p_1 $$
这是直线的参数方程。p₀ 和 p₁ 控制路径的形状,称为 控制点。
如果有三个控制点 $p_0, p_1, p_2$,我们可以构造一条 二次贝塞尔曲线:
$$ p(t) = (1 - t)^2 p_0 + 2t(1 - t) p_1 + t^2 p_2 $$
其中,$(1 - t)^2$、$2t(1 - t)$、$t^2$ 是 Bernstein 基函数。
贝塞尔曲线的优势在于:通过调整控制点可以直观地改变曲线形状,这在字体设计和汽车建模中非常有用。
5. Hermite 基多项式与 Hermite 插值
Hermite 插值允许我们用两个点 $p(0)$、$p(1)$ 及其切线斜率来表示任意三次多项式。
假设粒子运动轨迹为:
$$ p(t) = at^3 + bt^2 + ct + d $$
其一阶导数为:
$$ p'(t) = 3at^2 + 2bt + c $$
已知:
$$ \begin{align*} p(0) &= d \ p(1) &= a + b + c + d \ p'(0) &= c \ p'(1) &= 3a + 2b + c \end{align*} $$
将其写成矩阵形式:
$$ \begin{bmatrix} p(0) \ p(1) \ p'(0) \ p'(1) \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 & 1 \ 1 & 1 & 1 & 1 \ 0 & 0 & 1 & 0 \ 3 & 2 & 1 & 0 \end{bmatrix} \begin{bmatrix} a \ b \ c \ d \end{bmatrix} $$
解这个方程组后,可得 Hermite 插值的基函数:
$$ p(t) = \begin{bmatrix} 2t^3 - 3t^2 + 1 & -2t^3 + 3t^2 & t^3 - 2t^2 + t & t^3 - t^2 \end{bmatrix} \begin{bmatrix} p(0) \ p(1) \ p'(0) \ p'(1) \end{bmatrix} $$
6. 样条函数
样条函数是最常见的分段多项式插值方法。一个 k 次样条函数 $S(x)$ 在给定的节点 $\Delta = {x_0 < x_1 < \ldots < x_n}$ 上由 n 个子曲线组成,每个子曲线是 k 次多项式。
6.1 三次样条插值
三次样条插值使用三次多项式来连接相邻节点,满足以下条件:
- 每个区间上的 $S_j(x)$ 是三次多项式。
- $S_j(x_j) = y_j$
- $S_j(x_{j+1}) = S_{j+1}(x_{j+1})$,且一阶和二阶导数连续。
这保证了整个曲线的 $C^2$ 连续性。
6.2 三次样条的构造
设:
$$ S_j(x) = a_j + b_j(x - x_j) + c_j(x - x_j)^2 + d_j(x - x_j)^3 $$
每个区间有 4 个未知参数,共 4n 个参数。通过插值条件和连续性条件,可以建立关于 $c_j$ 的线性方程组:
$$ h_{j-1} c_{j-1} + 2(h_{j-1} + h_j)c_j + h_j c_{j+1} = \frac{3}{h_j}(a_{j+1} - a_j) - \frac{3}{h_{j-1}}(a_j - a_{j-1}) $$
6.3 自然三次样条
自然三次样条额外添加边界条件:
$$ S''(a) = 0,\quad S''(b) = 0 $$
这将方程组变为三对角矩阵形式,可用高斯消元法求解。
例如,给定数据点 $(0,0), (\pi/2,1), (\pi,0), (3\pi/2,-1), (2\pi,0)$ 构造自然三次样条逼近 $\sin x$,可得如下样条函数:
$$ S(x) = \begin{cases} 0.9549x - 0.1290x^3, & x \in [0, \pi/2] \ 1 - 0.6079x^2 + 0.129x^3, & x \in [\pi/2, \pi] \ -0.9549x + 0.1290x^3, & x \in [\pi, 3\pi/2] \ -1 + 0.6079x^2 - 0.1290x^3, & x \in [3\pi/2, 2\pi] \end{cases} $$
6.4 各类插值方法对比
| 方法 | 是否插值所有控制点 | 是否局部控制 | 连续性 |
|---|---|---|---|
| 自然样条 | ✅ | ❌ | $C^2$ |
| B 样条 | ❌ | ✅ | $C^2$ |
| 贝塞尔曲线 | ✅(端点) | ❌ | $C^1$ |
| 分段 Hermite | ✅(端点) | ✅ | $C^1$ |
7. 应用场景
- 自然样条:适用于需要全局光滑插值的场合,如金融曲线拟合。
- 贝塞尔曲线:广泛用于字体设计、图形软件(如 Adobe Illustrator)。
- B 样条:用于 CAD 设计,支持局部控制和高阶连续性。
- Hermite 插值:适合需要指定端点切线的动画路径设计。
例如,著名的 Utah Teapot 就是使用贝塞尔曲面建模的:

8. 总结
本文介绍了几种常见的分段插值方法:
- 贝塞尔曲线:通过端点和控制点构造,适合图形设计。
- Hermite 插值:通过端点及其切线构造,适合动画路径。
- 自然三次样条:全局 $C^2$ 连续,但修改一个点会影响整体。
- B 样条:局部控制,适合复杂建模。
每种方法都有其适用场景,理解它们的数学原理有助于我们在实际开发中做出更合适的选择。