Left Factoring vs. Left Recursion

1. Introduction

In this tutorial, we’ll discuss two critical grammar concepts in compiler design: left recursion and left factoring. We’ll explore their core differences and explain how to optimize parsing performance.

2. Left Recursion

Left recursion occurs when a non-terminal symbol in a grammar rule refers to itself as the leftmost symbol in its production:

$[A \rightarrow A\alpha \mid \beta]$

Here, A is a non-terminal, $\alpha$ is a non-empty string, whereas $\beta$ is a string that can be empty.

Furthermore, left recursion can be direct, as illustrated above, or indirect, where a non-terminal eventually refers back to itself through a chain of productions. For example:

$[\begin{aligned} A &\rightarrow B\alpha \\ B &\rightarrow A\beta \end{aligned}]$

This recursion is indirect because A depends on B, which depends on A.

2.1. Why Is Left Recursion a Problem?

When some parsers attempt to parse input based on a left-recursive rule, such as $A \rightarrow A' \alpha$ , they can get stuck in an infinite loop, repeatedly trying to match A without ever reaching $\beta$ . This problem is common in top-down parsers (like recursive descent parsers), which expand rules starting from the left side:

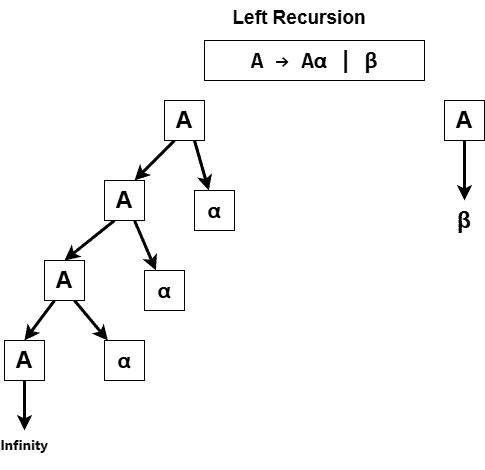
Left-Recursion

This is the case with top-down parsers, such as LL parsers. These parsers try to predict which rule to apply based on the next input token, moving from left to right. However, they can’t do that with a left-recursive rule, as they keep “recursing” without progressing through the input string. As a result, we get an infinite loop in the parser.

For instance, let’s say we have a left-recursive rule for parsing a list of terms separated by commas:

$[\text{List} \rightarrow \text{List} \, ',' \, \text{Term} \mid \text{Term}]$

With this rule, the parser starts by trying to match List. Since it also sees List on the right-hand side, it tries to match it again, creating a never-ending cycle.

2.2. How to Eliminate Left Recursion?

We need to eliminate left recursion to make a grammar compatible with LL parsing. The general approach involves restructuring the rules so that recursion happens at the end of a production rather than at the beginning.

For instance, for a rule such as:

$[A \rightarrow A\alpha \mid \beta]$

the trick is to replace it with:

$[\begin{aligned} A &\rightarrow \beta A' \\ A' &\rightarrow \alpha A' \mid \varepsilon \end{aligned}]$

This new setup uses a helper non-terminal, A′, which lets us handle the recursion “from the right” instead of directly looping back to A (and $\varepsilon$ denotes the empty string).

For example, suppose the input is cdd, and the grammar before elimination is:

$[\begin{aligned} A &\rightarrow A\alpha \mid \beta \\ \alpha &= d, \quad \beta = c \end{aligned}]$

Using the left-recursive rule, a top-down parser would attempt:

$[A \rightarrow A\alpha \rightarrow A\alpha\alpha \rightarrow A\alpha\alpha\alpha \rightarrow \ldots \text{ (infinite recursion)}]$

But after eliminating left recursion, the grammar becomes:

$[\begin{aligned} A &\rightarrow \beta A' \\ A' &\rightarrow \alpha A' \mid \epsilon \\ \alpha &= d, \quad \beta = c \end{aligned}]$

For our previous input cdd, parsing now proceeds as:

$[\begin{aligned} A &\rightarrow \beta A' \rightarrow c A' \\ A' &\rightarrow \alpha A' \rightarrow d A' \\ A' &\rightarrow \alpha A' \rightarrow d A' \\ A' &\rightarrow \epsilon \text{ (ending recursion)} \end{aligned}]$

Therefore, the transformation ensures the input cdd is successfully parsed, avoiding infinite recursion and making the grammar suitable for LL parsers.

3. Left Factoring

Left factoring is a technique that simplifies grammar rules to make parsing more efficient and less error-prone. This approach is especially helpful for top-down parsers, which can run into trouble when faced with ambiguous or left-recursive grammars.

The basic idea behind left factoring is to rewrite the rules that share beginnings (prefixes) so that the parser doesn’t need to backtrack or guess which rule to apply.

3.1. Why Do We Use Left Factoring?

Top-down parsers process input by scanning symbols from left to right and matching them against the grammar rules. If two or more rules start with the same symbols, the parser can’t immediately decide which one to follow. This results in backtracking or even parsing errors, making the process less efficient.

Left factoring removes this ambiguity by isolating the common parts of rules, reducing the need for the parser to backtrack. With left factoring, we get a clear, step-by-step process that the parser can follow smoothly.

Let’s look at this grammar that’s not left-factored:

$[A \rightarrow \alpha \beta \mid \alpha \gamma]$

In this example, both rules for A start with the symbol $\alpha$ . Without left factoring, the parser has to guess or backtrack after reading $\alpha$ , which can lead to parsing issues.

To apply left factoring, we rewrite this rule to group the common prefix $\alpha$ :

$[\begin{aligned} A &\rightarrow \alpha A' \\ A' &\rightarrow \beta \mid \gamma \end{aligned}]$

Now, the parser matches $\alpha$ and then decides between $\beta$ and $\gamma$ based on what follows. This way, the parser no longer needs to backtrack, so parsing is smoother.

3.2. Example

Let’s consider the input ab and the following grammar that’s not left-factored:

$[\begin{aligned} A &\rightarrow \alpha \beta \mid \alpha \gamma \\ \alpha &= a, \quad \beta = b, \quad \gamma = c \end{aligned}]$

For the input ab, a top-down parser without left factoring faces the following challenges:

After reading a ( $\alpha$ ), it cannot immediately determine whether to follow $A \rightarrow \alpha \beta$ or $A \rightarrow \alpha \gamma$ because both start with a
The parser must backtrack or use lookahead to resolve the ambiguity, complicating the parsing

By applying left factoring, we rewrite the grammar as follows:

$[\begin{aligned} A &\rightarrow \alpha A' \\ A' &\rightarrow \beta \mid \gamma \end{aligned}]$

Now, parsing the input ab is straightforward:

$[\begin{aligned} A &\rightarrow \alpha A', \quad A' \rightarrow a A' \\ A' &\rightarrow \beta, \quad \beta \rightarrow b \end{aligned}]$

This process is direct and eliminates the need for backtracking. The parser first matches the common prefix a and then distinguishes between $\beta$ and $\gamma$ based on what follows, ensuring efficient parsing.

In general, left factoring reduces ambiguity, eliminates the need for backtracking, and simplifies the implementation of LL parsers.

4. Key Differences Between Left Factoring and Left Recursion

Left factoring and left recursion are distinct concepts in grammar design with different impacts on parser efficiency and compatibility:

Aspect

Left Recursion

Left Factoring

Definition

Non-terminal appears as the leftmost symbol in its production.

Eliminates common prefixes in productions.

Purpose

Expresses repetitive structures.

Reduces ambiguity and improves parser efficiency.

Impact on Grammar

It makes grammar unsuitable for top-down parsers.

Introduces new non-terminals for common prefixes.

Parser Efficiency

Causes infinite loops in top-down parsers.

Improves efficiency by reducing choices.

Ambiguity Resolution

Introduces ambiguity if not handled properly.

Helps resolve ambiguity.

Compatibility

Incompatible with top-down parsers and requires elimination.

Compatible with both top-down and bottom-up parsers.

Left factoring improves grammar clarity and efficiency, while left recursion can cause issues for top-down parsers.

5. Conclusion

In this article, we discussed two important concepts in the design of formal grammars: left recursion and left factoring. Left factoring is a technique used to eliminate common prefixes in productions, improving grammar clarity and parser efficiency. It’s compatible with both top-down and bottom-up parsers and helps resolve ambiguity.

On the other hand, left recursion, where a non-terminal appears as the leftmost symbol in its production, can express repetitive structures but causes issues for top-down parsers by potentially leading to infinite loops. While left recursion is generally incompatible with top-down parsers, it can be handled by bottom-up parsers without modification.

Persistence

REST

Security