1. Introduction
Stacks are a fundamental data structure in computer science, commonly used for problems involving Last-In-First-Out (LIFO) operations. However, in certain scenarios, a more structured approach is needed to process elements in a specific order efficiently. This is where the Monotonic Stack comes in.
Monotonic stacks allow certain operations to be performed in linear time, making them significantly more efficient than brute-force approaches.
In this tutorial, we’ll explore how a monotonic stack works, its different types, and its practical applications in algorithmic problem-solving.
2. What Is a Monotonic Stack?
A monotonic stack is a variation of a standard stack that maintains its elements in a specific order, either increasing or decreasing. The term “monotonic” refers to the fact that elements are always arranged in a single, non-changing order as new elements are pushed and old ones are popped. This structure allows for efficient processing of certain problems that require comparisons between elements, such as finding the next greater or smaller element in an array.
There are two types of monotonic stacks: monotonically increasing and monotonically decreasing.
A monotonically increasing stack ensures that elements are stored in non-decreasing order. When a new element is pushed, any smaller elements already in the stack are removed to maintain the increasing order.
A monotonically decreasing stack maintains elements in non-increasing order. When pushing a new element, any larger elements already in the stack are popped to enforce the decreasing order.
The core idea behind a monotonic stack is that each element is processed in a way that ensures efficient lookups while preserving order. Instead of checking every possible pair in an array, the stack helps eliminate unnecessary comparisons, leading to an optimal O(n) time complexity.
3. How Does a Monotonic Stack Work?
A monotonic stack processes elements while maintaining a specific order, either increasing or decreasing. Instead of checking every pair of elements in a brute-force manner, it removes unnecessary elements dynamically, allowing for an efficient O(n) time complexity.
3.1. Maintaining Monotonic Order
The core idea behind a monotonic stack is that elements are pushed and popped in a way that preserves a specific order. When a new element is encountered, the stack checks whether it violates the order. If it does, elements are removed until the order is restored.
For a monotonically increasing stack, elements are stored in non-decreasing order. When a new element is pushed, any smaller elements already in the stack are removed. This ensures that every element in the stack is always larger than or equal to the one below it.
For a monotonically decreasing stack, elements are stored in non-increasing order. When a new element is pushed, any larger elements already in the stack are removed to maintain the decreasing sequence.
3.2. Example Walkthrough
Suppose we have a stack with the numbers 1, 4, 5, 3, 12, 10. Let’s analyze how these values are processed using both monotonically increasing and monotonically decreasing stacks:
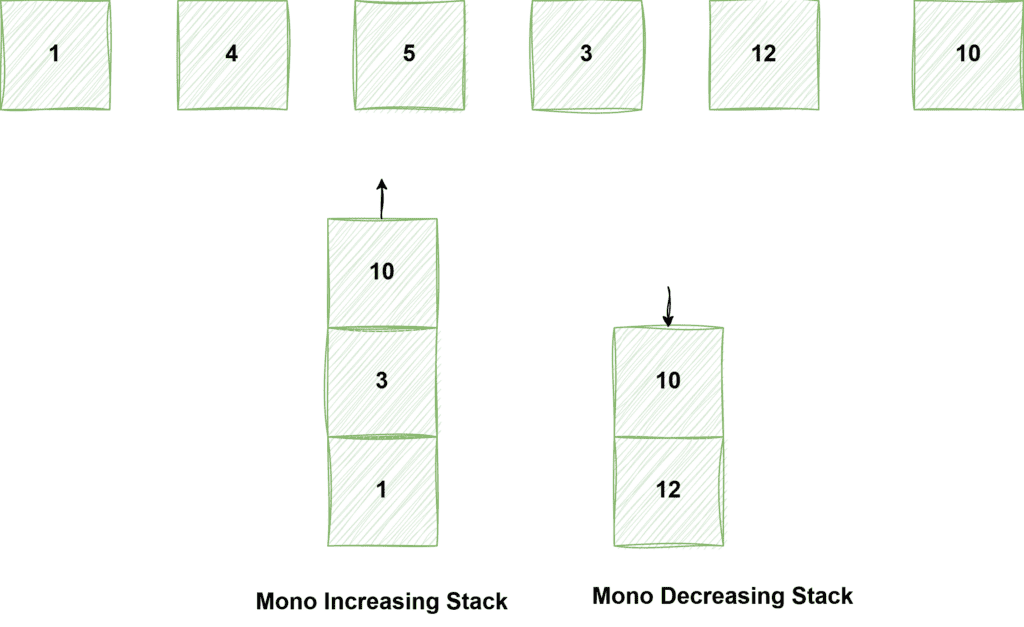
In a monotonically increasing stack, we push elements such that the stack maintains a non-decreasing order. If a smaller element appears, we pop larger elements until the stack is in order. We push 1 first, so the stack is 1. We then push 4, as 4 is greater than 1, making the stack [1, 4]. Next, we push 5, as 5 is greater than 4, and the stack becomes [1, 4, 5]. When we encounter 3, it’s smaller than 5 and 4, so we pop 5 and 4, then push 3, resulting in [1, 3]. We push 12, as it’s greater than 3, making the stack [1, 3, 12]. Finally, when we encounter 10, it’s smaller than 12, so we pop 12 and push 10, and the stack becomes [1, 3, 10]. The final stack is [1, 3, 10].
In a monotonically decreasing stack, we maintain a non-increasing order. When a larger element appears, we pop it before pushing the smaller one. We push 1 first, so the stack is [1]. Then, we push 4. Since 4 is greater than 1, we pop 1 and push 4, making the stack [4]. We then push 5, and since 5 is greater than 4, we pop 4 and push 5, so the stack becomes [5]. Next, we push 3, as it’s smaller than 5, so the stack is [5, 3]. We push 12, and since it’s larger than both 3 and 5, we pop both and push 12, resulting in [12]. Finally, we push 10, as it’s smaller than 12, making the stack [12, 10]. The final stack is [12, 10].
3.3. Why Is It Efficient?
Each element is pushed and popped at most once, meaning the total number of operations is proportional to the number of elements in the array. Since the stack removes elements only when necessary, it avoids redundant comparisons, reducing unnecessary computations.
By maintaining a monotonic order and ensuring that only relevant elements remain in the stack, this technique provides an elegant and optimized solution for many problems involving element comparisons.
4. Example Problems & Implementations
Understanding monotonic stacks is easier with practical examples. Below are two common problems where a monotonic stack provides an optimal solution.
4.1. Next Greater Element
The Next Greater Element problem asks us to find, for each element in an array, the next greater value that appears to its right. If no such value exists, we return -1.
A monotonically decreasing stack is used to track larger elements efficiently. As we iterate through the array, we remove elements from the stack if they are smaller than the current element. This ensures that each element is processed in constant time, leading to an O(n) complexity:
4.2. Next Smaller Element
The Next Smaller Element problem is similar but requires finding the next smaller value to the right of each element. Instead of a decreasing stack, we use a monotonically increasing stack, ensuring that the smallest elements are efficiently tracked:
5. Time Complexity Analysis
The efficiency of a monotonic stack comes from the fact that each element is processed only once. Every element is pushed onto the stack once and popped at most once, meaning the total number of operations is proportional to the number of elements in the input. This results in an time complexity, significantly better than a brute-force approach’s
complexity. In the worst case, the space complexity is
, where all elements are stored in the stack.
6. Conclusion
A monotonic stack is a powerful variation of the standard stack that maintains a strictly increasing or decreasing order. This simple yet effective structure solves a wide range of problems, such as finding the next greater or smaller element, computing the largest rectangle in a histogram, and optimizing stock span calculations. A monotonic stack provides an optimal solution with a time complexity of by ensuring that each element is processed efficiently.
In this article, we understand when to use a monotonic stack and how to implement it effectively, significantly enhancing our ability to solve complex problems efficiently.