How Bootstrapping Works in Machine Learning

1. Introduction

Although bootstrapping was first introduced in statistics, it has since gained popularity across many fields. In machine learning, some models like random forest incorporate bootstrapping in their core.

In this tutorial, we’ll explore bootstrapping and its importance in machine learning. We’ll focus on its role in ensemble methods, such as random forest and bagging. Then, we’ll highlight the key differences between cross-validation and bootstrapping, a common source of confusion.

2. Bootstrapping in Machine Learning

Let’s begin with a clear and straightforward definition. Bootstrapping is a resampling technique that estimates a statistic’s distribution by repeatedly drawing random samples with replacements from the original dataset.

Let’s look at an example.

2.1. Customer Satisfaction Example

Suppose we analyze customer satisfaction for a small company with limited customers and resources. We collected 15 responses on a scale from 1 (very dissatisfied) to 5 (very satisfied), with 3 representing a neutral opinion. Interestingly, we received exactly three responses for each rating, resulting in the following histogram:

It’s clear that drawing conclusions from this plot—or even from the mean (which is 3)—is challenging. Additionally, we might ask: How uncertain is our estimate? How much would the mean change if we sampled a different group of customers?

2.2. Bootstrapping Steps

Instead of conducting new trials, which can be costly and time-consuming, we employ bootstrapping to simulate the process. The procedure consists of three main steps:

1. Random Sampling: We randomly select 15 customers from the original dataset, allowing replacements. Some customers appear multiple times, while others get excluded. We then calculate the mean satisfaction score for this new group
2. Repetition: We repeat this resampling process thousands of times — in our case, 3,000 iterations. In each iteration, we calculate a new mean satisfaction score
3. Building the Distribution: Finally, we aggregate all the mean scores from the previous step to create a distribution. This distribution represents the variability in the average satisfaction across all resampled groups

This method gives us a robust estimate of the average satisfaction score and its distribution without the need for additional trials: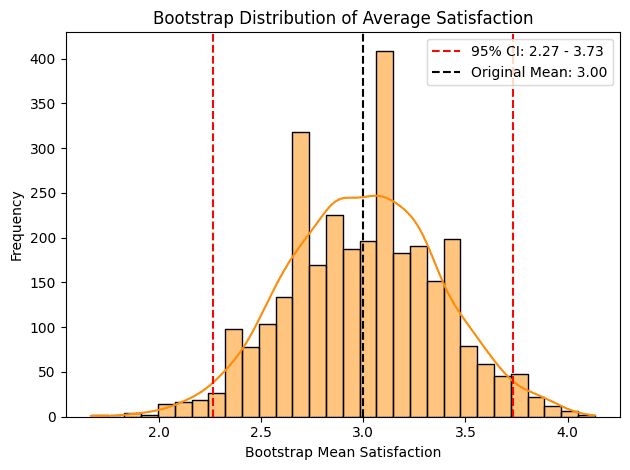

Rather than relying on a single estimate of customer satisfaction from just one trial, we can compute confidence intervals to provide a more reliable measure. For example, we can say, “We are 95% confident that the customers’ satisfaction lies between 2.27 and 3.73”.

This approach presents the results and gives insight into their reliability, allowing us to quantify the uncertainty surrounding the estimate. Now, let’s examine how bootstrapping works for ensemble methods.

2.3. Bagging (Bootstrap Aggregating)

Bagging is an ensemble method in which base models (e.g., decision trees and SVMs) train on bootstrap samples. These are random data subsets taken with replacement, each matching the original dataset’s size.

For decision trees, each tree trains on a unique, random data subset. As a result, this variation helps prevent overfitting to noise or specific patterns. Then, the model combines final predictions using majority vote (classification) or averaging (regression). This process reduces variance and improves generalization.

2.4. Random Forest

For random forests, in addition to using bootstrap samples, we can select a subset of features for each decision tree. Each tree trains on a bootstrap sample and a random subset of features at every split. This process ensures diversity, as trees see different data points and features, reducing reliance on dominant predictors.

The model randomly selects feature subsets to complement bootstrapped data. These two levels of randomness build an ensemble of uncorrelated, high-bias/low-variance trees that are ready for aggregation. The model then makes final predictions using majority vote or averaging.

2.5. Other Methods

Besides ensemble methods, we can find other machine learning applications that use bootstrapping. We can train neural networks in deep learning using bootstrapped datasets and average predictions. We can even use bootstrapped samples in linear models that use logistic or ridge regression.

Bootstrapping helps estimate uncertainty and make models more reliable, but it can be costly. Still, its benefits—like better confidence intervals and variance estimates—often make it worth using in machine learning. However, many people confuse bootstrapping with cross-validation, so let’s clear up the difference.

3. Cross-Validation vs. Bootstrapping

Both bootstrapping and cross-validation help us resample data in machine learning, but they serve different goals. We use bootstrapping to estimate uncertainty, while cross-validation helps us evaluate model performance and prevent overfitting.

Let’s break it down. Bootstrapping works by randomly sampling data with replacement, creating multiple datasets to assess variability. Conversely, cross-validation splits the dataset into folds, training the model on different subsets to ensure a more reliable evaluation.

Their applications also differ. Bootstrapping is key in ensemble methods like Random Forest and Bagging, where multiple models learn from varied training sets. Cross-validation is essential for model selection, helping us fine-tune hyperparameters and avoid overfitting.

Another big difference is how we handle training data. In bootstrapping, the training set keeps the same size as the original, but some samples appear multiple times while others stay out (out-of-bag samples). In cross-validation, each fold reduces the training size, ensuring the model tests every data point at least once. Let’s see an example.

3.1. Example

To make the concept easier to digest, let’s look at an example in which we have six data points , each associated with a corresponding target value , which we omit for simplicity.

In Bootstrapping, we sample with replacement. So, we can have two boostrapped samples with the same size as the original dataset. We define the first boostrapped sample and the second sample . One key aspect of bootstrapping is that some data points may not appear in a given sample, while others could be repeated.

We then train two separate models, each using a different bootstrapped sample. Since each model is trained on a slightly different subset of data, they will vary in their performance. The primary benefit of this approach is that it allows us to estimate uncertainty by evaluating the models on different samples.

In cross-validation, we split the dataset into two folds: and . We now perform a -fold cross-validation. We start by training the first model on and testing it on . Then, we train the second model on and test it on . This ensures that each data point gets a chance to be used for both training and testing.

4. Conclusion

In this article, we explored bootstrapping and its role in machine learning. Bootstrapping plays a key role in bagging models and adds randomness to random forests. We also compared cross-validation and bootstrapping, which are both resampling techniques. Cross-validation helps evaluate models, while bootstrapping estimates uncertainty.